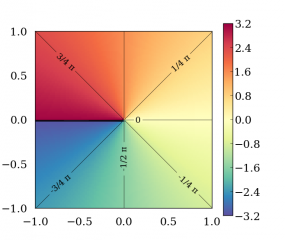
std::atan2, std::atan2f, std::atan2l

 

C++

編譯器支援

自由（freestanding）與宿主（hosted）

語言

標準庫

標準庫標頭檔案

具名要求

特性測試宏 (C++20)

語言支援庫

概念庫 (C++20)

診斷庫

記憶體管理庫

超程式設計庫 (C++11)

通用工具庫

容器庫

迭代器庫

範圍庫 (C++20)

演算法庫

字串庫

文字處理庫

數值庫

日期和時間庫

輸入/輸出庫

檔案系統庫 (C++17)

併發支援庫 (C++11)

執行控制庫 (C++26)

技術規範

符號索引

外部庫

 

數值庫

常用數學函式
數學特殊函式 (C++17)
數學常數 (C++20)
基本線性代數演算法 (C++26)
資料並行型別 (SIMD) (C++26)
浮點環境 (C++11)
複數
數值陣列 (valarray)
偽隨機數生成
位操作 (C++20)
因子運算
gcd (C++17)	lcm (C++17)
插值
midpoint (C++20)	lerp (C++20)
飽和算術
add_sat (C++26) sub_sat (C++26) saturate_cast (C++26)	mul_sat (C++26) div_sat (C++26)
通用數值運算
iota (C++11) ranges::iota (C++23) accumulate inner_product adjacent_difference    partial_sum	reduce (C++17) transform_reduce (C++17) inclusive_scan (C++17) exclusive_scan (C++17) transform_inclusive_scan (C++17) transform_exclusive_scan (C++17)

 

常用數學函式

函式
基本操作
abs(int)labsllabsimaxabs (C++11)   abs(float)fabs divldivlldivimaxdiv (C++11)	fmod remainder (C++11)   remquo (C++11) fma (C++11) fmax (C++11) fmin (C++11) fdim (C++11) nannanfnanl (C++11)(C++11)(C++11)
指數函式
exp exp2 (C++11) expm1 (C++11)	log log10 log1p (C++11) log2 (C++11)
冪函式
sqrt cbrt (C++11)	hypot (C++11) pow
三角和 雙曲函式
sin cos tan asin acos atan atan2	sinh cosh tanh asinh (C++11) acosh (C++11) atanh (C++11)
誤差函式和伽馬函式
erf (C++11) erfc (C++11)	lgamma (C++11) tgamma (C++11)

取整浮點運算
ceil floor roundlroundllround (C++11)(C++11)(C++11)	trunc (C++11) nearbyint (C++11) rintlrintllrint (C++11)(C++11)(C++11)
浮點操縱函式
ldexp scalbnscalbln (C++11)(C++11) ilogb (C++11) logb (C++11)	frexp modf nextafternexttoward (C++11)(C++11) copysign (C++11)
分類和比較
fpclassify (C++11) isfinite (C++11) isinf (C++11) isnan (C++11) isnormal (C++11) signbit (C++11)	isgreater (C++11) isgreaterequal (C++11) isless (C++11) islessequal (C++11) islessgreater (C++11) isunordered (C++11)
型別
div_t ldiv_t lldiv_t (C++11)	imaxdiv_t (C++11) float_t (C++11) double_t (C++11)
宏常量
HUGE_VALFHUGE_VALHUGE_VALL (C++11)(C++11) math_errhandlingMATH_ERRNOMATH_ERREXCEPT (C++11)   INFINITY (C++11) NAN (C++11)	分類 FP_NORMALFP_SUBNORMALFP_ZEROFP_INFINITEFP_NAN (C++11)(C++11)(C++11)(C++11)(C++11)

 

定義於標頭檔案 <cmath>
	(1)
float       atan2 ( float y, float x ); double      atan2 ( double y, double x ); long double atan2 ( long double y, long double x );			(直至 C++23)
/*floating-point-type*/             atan2 ( /*floating-point-type*/ y,                     /*floating-point-type*/ x );			(C++23 起) (C++26 起為 constexpr)
float       atan2f( float y, float x );		(2)	(C++11 起) (C++26 起為 constexpr)
long double atan2l( long double y, long double x );		(3)	(C++11 起) (C++26 起為 constexpr)
SIMD 過載 (C++26 起)
定義於標頭檔案 <simd>
template< class V0, class V1 > constexpr /*math-common-simd-t*/<V0, V1>             atan2 ( const V0& v_y, const V1& v_x );		(S)	(C++26 起)
額外過載 (自 C++11 起)
定義於標頭檔案 <cmath>
template< class Integer > double      atan2 ( Integer y, Integer x );		(A)	(C++26 起為 constexpr)

1-3) 使用引數的符號計算 y / x 的反正切，以確定正確的象限。 庫為所有 cv-unqualified 浮點型別的引數提供了 std::atan2 的過載。(C++23 起)

S) SIMD 過載對 v_y 和 v_x 執行逐元素 std::atan2。 (參閱 math-common-simd-t 的定義。)

(C++26 起)

A) 為所有整數型別提供了額外的過載，它們被視為 double。

(C++11 起)

引數

y, x

-

浮點數或整數值

返回值

如果沒有錯誤發生，則返回 y / x 的反正切（arctan(

y

x

)），其範圍在 [-π, +π] 弧度內。

y 引數

返回值

x 引數

如果發生域錯誤，則返回實現定義的值 (支援 NaN 時返回 NaN)。

如果因下溢發生範圍錯誤，則返回正確結果（舍入後）。

錯誤處理

錯誤按 math_errhandling 指定的方式報告。

如果 x 和 y 都為零，可能會發生定義域錯誤。

如果實現支援 IEEE 浮點運算 (IEC 60559)，

• 如果 x 和 y 都為零，則*不會*發生定義域錯誤。
• 如果 x 和 y 都為零，也不會發生值域錯誤。
• 如果 y 為零，則不會發生極點錯誤。
• 如果 y 為 ±0 且 x 為負數或 -0，則返回 ±π。
• 如果 y 為 ±0 且 x 為正數或 +0，則返回 ±0。
• 如果 y 為 ±∞ 且 x 為有限值，則返回 ±π/2。
• 如果 y 為 ±∞ 且 x 為 -∞，則返回 ±3π/4。
• 如果 y 為 ±∞ 且 x 為 +∞，則返回 ±π/4。
• 如果 x 為 ±0 且 y 為負數，則返回 -π/2。
• 如果 x 為 ±0 且 y 為正數，則返回 +π/2。
• 如果 x 為 -∞ 且 y 為有限正數，則返回 +π。
• 如果 x 為 -∞ 且 y 為有限負數，則返回 -π。
• 如果 x 為 +∞ 且 y 為有限正數，則返回 +0。
• 如果 x 為 +∞ 且 y 為有限負數，則返回 -0。
• 如果 x 或 y 為 NaN，則返回 NaN。

注意

std::atan2(y, x) 等價於 std::arg(std::complex<std::common_type_t<decltype(x), decltype(y)>>(x, y))。

POSIX 指定，在下溢的情況下，返回 y / x 的值；如果不支援，則返回一個不大於 DBL_MIN、FLT_MIN 和 LDBL_MIN 的實現定義值。

不要求完全按照 (A) 提供額外的過載。它們只需要足以確保其第一個引數 num1 和第二個引數 num2

如果 num1 或 num2 的型別為 long double，則 std::atan2(num1, num2) 的效果與 std::atan2(static_cast<long double>(num1),            static_cast<long double>(num2)) 相同。 否則，如果 num1 和/或 num2 的型別為 double 或整型，則 std::atan2(num1, num2) 的效果與 std::atan2(static_cast<double>(num1),            static_cast<double>(num2)) 相同。 否則，如果 num1 或 num2 的型別為 float，則 std::atan2(num1, num2) 的效果與 std::atan2(static_cast<float>(num1),            static_cast<float>(num2)) 相同。

(直至 C++23)

如果 num1 和 num2 具有算術型別，則 std::atan2(num1, num2) 的效果與 std::atan2(static_cast</*common-floating-point-type*/>(num1),            static_cast</*common-floating-point-type*/>(num2)) 相同，其中 /*common-floating-point-type*/ 是具有 num1 和 num2 型別之間最高浮點轉換等級和最高浮點轉換子等級的浮點型別，整型引數被視為與 double 具有相同的浮點轉換等級。 如果不存在具有最高等級和次等級的浮點型別，則過載決議不會從提供的過載中產生可用的候選函式。

(C++23 起)

示例

執行此程式碼

#include <cmath>
#include <iostream>
 
void print_coordinates(int x, int y)
{
    std::cout << std::showpos
              << "(x:" << x << ", y:" << y << ") cartesian is "
              << "(r:" << std::hypot(x, y)
              << ", phi:" << std::atan2(y, x) << ") polar\n";
}
 
int main()
{
    // normal usage: the signs of the two arguments determine the quadrant
    print_coordinates(+1, +1); // atan2( 1,  1) =  +pi/4, Quad I
    print_coordinates(-1, +1); // atan2( 1, -1) = +3pi/4, Quad II
    print_coordinates(-1, -1); // atan2(-1, -1) = -3pi/4, Quad III
    print_coordinates(+1, -1); // atan2(-1,  1) =  -pi/4, Quad IV
 
    // special values
    std::cout << std::noshowpos
              << "atan2(0, 0) = " << atan2(0, 0) << '\n'
              << "atan2(0,-0) = " << atan2(0, -0.0) << '\n'
              << "atan2(7, 0) = " << atan2(7, 0) << '\n'
              << "atan2(7,-0) = " << atan2(7, -0.0) << '\n';
}

輸出

(x:+1, y:+1) cartesian is (r:1.41421, phi:0.785398) polar
(x:-1, y:+1) cartesian is (r:1.41421, phi:2.35619) polar
(x:-1, y:-1) cartesian is (r:1.41421, phi:-2.35619) polar
(x:+1, y:-1) cartesian is (r:1.41421, phi:-0.785398) polar
atan2(0, 0) = 0
atan2(0,-0) = 3.14159
atan2(7, 0) = 1.5708
atan2(7,-0) = 1.5708

參閱

asinasinfasinl (C++11)(C++11)	計算反正弦（\({\small\arcsin{x}}\)arcsin(x)） (函式)
acosacosfacosl (C++11)(C++11)	計算反餘弦（\({\small\arccos{x}}\)arccos(x)） (函式)
atanatanfatanl (C++11)(C++11)	計算反正切（\({\small\arctan{x}}\)arctan(x)） (函式)
arg	返回相角 (函式模板)
atan2(std::valarray)	將函式 std::atan2 應用於 valarray 和一個值 (函式模板)
C 文件 關於 atan2